PyTorch 2.x and Backends (WIP, come back in a couple of days)
Disclaimer: Human “generated” text as a labor of love.
The Great ML Framework Debate
Centuries ago (2020), I contributed to PyTorch library, specifically, TorchServe which used to be the default model serving library for PyTorch Models.
Back then the ML Frameworks were split into two factions:
- Eager Mode
- Graph Mode
Graph Mode was a strict programming model which required the models to be expressible as compute DAGs. With each node of the graph expresed as a single operation whose inputs and outputs were statically sized. This made life easier for the frameworks to optimize with a compiler since graph optimizations are readily achievable offline in comparison to dynamic shapes. This can be seen as analogous to programming in statically typed languages such as C/C++. ML Frameworks in question are TensorFlow 1.x, MxNet etc
Eager Mode was easier to code and debug with. Preferred by users who just wanted to get on with it. If you are concerned more with the outcome of the model you are building then this is how you would be thinking. It was analogous to programming with Python. PyTorch was the flagbearer for this eager mode, funnily enough MxNet also supported this.
PyTorch - Graph Modes
PyTorch wanted in, so they made all these different attempts at also becoming a Graph Mode Execution Framework.
torch.jit.tracetorch.jit.scriptLazy Tensors
But the users were not interested.
PyTorch Compile
In PyTorch 2.x, we have the option to compile the model and make faster where we can. In the sense, not all parts of the model can be captured as a graph but whatever can be captured can be optimized.
# model is your model torch.nn.Module
compiled_model = torch.compile(model, backend="inductor", mode="max-autotune", dynamic=True)This script tests the dynamic compilation feature of PyTorch with a large tensor.
It uses the torch.compile decorator to compile a function that computes
the sine and cosine of a tensor, and then calls this function with a large tensor
on a CUDA device.
TorchDynamo:
Graph Capture for PyTorch inside torch.compile
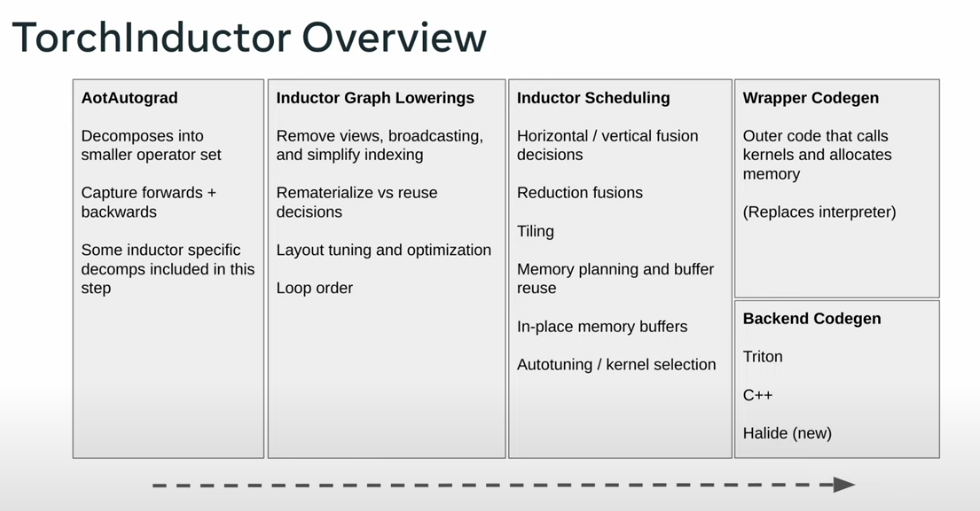
TorchInductor:
Default compiler backend for PyTorch.
Defining Custom Backend For torch.compile()
In Tesla Autopilot, we use a custom ASIC / Inference Computer on-board. We always wanted to define a backend so the model’s compilation stack could be abstracted away from the Model Developers. But the constraints of the hardware required us to do operations (model partitioning, sometimes, by hand) which were done better when compiled statically offline.
Here, we will see how a simple user-defined backend would look. In a real world backend, these sample inputs will be used to implement optimizations. Again, notice that optimizations are possible only when input shapes and sizes are known.
from typing import List
import torch
def my_compiler(gm: torch.fx.GraphModule,
sample_inputs: List[torch.Tensor]):
print("my_compiler() called with FX graph:")
gm.graph.print_tabular()
return gm # returns a callable
@torch.compile(backend=my_compiler)
def toy_example(a, b):
x = a / (torch.abs(a) + 1)
if b.sum() < 0:
b = b * -1
return x * b
for _ in range(1000):
toy_example(torch.randn(10), torch.randn(10))
from typing import List
import torch
def my_compiler(gm: torch.fx.GraphModule,
sample_inputs: List[torch.Tensor]):
print("my_compiler() called with FX graph:")
gm.graph.print_tabular()
return gm # returns a callable
@torch.compile(backend=my_compiler)
def toy_example(a, b):
x = a / (torch.abs(a) + 1)
if b.sum() < 0:
b = b * -1
return x * b
for _ in range(1000):
toy_example(torch.randn(10), torch.randn(10))my_compiler() called with FX graph:
opcode name target args kwargs
------------- ------ ------------------------------------------------------ ----------- --------
placeholder l_a_ L_a_ () {}
placeholder l_b_ L_b_ () {}
call_function abs_1 <built-in method abs of type object at 0x7fdce4beff00> (l_a_,) {}
call_function add <built-in function add> (abs_1, 1) {}
call_function x <built-in function truediv> (l_a_, add) {}
call_method sum_1 sum (l_b_,) {}
call_function lt <built-in function lt> (sum_1, 0) {}
output output output ((x, lt),) {}
my_compiler() called with FX graph:
opcode name target args kwargs
------------- ------ ----------------------- ----------- --------
placeholder l_b_ L_b_ () {}
placeholder l_x_ L_x_ () {}
call_function b <built-in function mul> (l_b_, -1) {}
call_function mul_1 <built-in function mul> (l_x_, b) {}
output output output ((mul_1,),) {}
my_compiler() called with FX graph:
opcode name target args kwargs
------------- ------ ----------------------- ------------ --------
placeholder l_x_ L_x_ () {}
placeholder l_b_ L_b_ () {}
call_function mul <built-in function mul> (l_x_, l_b_) {}
output output output ((mul,),) {}
Let’s break this down:
Our toy_example function is basically being run with of two tensors of 10 random values each. The function as simple as it is, can be broadly divided into three parts:
COMPUTE 1
IF COND:
COMPUTE 2
COMPUTE 3
The three graphs printed in tabular form are actually just these COMPUTE1, COMPUTE2, COMPUTE3.
import torch
print(torch.__version__)2.6.0+cu124
import os
os.environ['TORCH_COMPILE_DEBUG'] = '1'
import torch
@torch.compile(dynamic=True)
def foo(x):
y = x.sin()
z = y.cos()
return y, z
foo(torch.randn([8192, 8192], device='cuda'))/home/mlaidev/software/jsr_gdm/.venv/lib/python3.13/site-packages/torch/utils/_config_module.py:342: UserWarning: Skipping serialization of skipfiles_inline_module_allowlist value {}
warnings.warn(
W0526 09:03:48.447000 189635 /home/mlaidev/software/jsr_gdm/.venv/lib/python3.13/site-packages/torch/_inductor/debug.py:435] [1/0] model__1_inference_1 debug trace: /home/mlaidev/software/jsr_gdm/pytorch_backend/torch_compile_debug/run_2025_05_26_09_03_06_493183-pid_189635/torchinductor/model__1_inference_1.1
(tensor([[-0.5081, 0.8742, -0.7563, ..., 0.7116, 0.6417, 0.8982],
[-0.1069, -0.9184, -0.6707, ..., -0.3978, -0.6187, 0.8878],
[ 0.6196, -0.6739, -0.4469, ..., 0.7490, -0.9443, 0.7898],
...,
[ 0.8925, -0.9631, -0.9991, ..., 0.3309, -0.1943, -0.1613],
[-0.9386, -0.8649, -0.9941, ..., 0.4611, -0.2239, 0.1002],
[ 0.6346, -0.2102, 0.8530, ..., -0.9979, -0.7121, -0.8892]],
device='cuda:0'),
tensor([[0.8737, 0.6416, 0.7274, ..., 0.7573, 0.8011, 0.6230],
[0.9943, 0.6071, 0.7834, ..., 0.9219, 0.8146, 0.6312],
[0.8141, 0.7814, 0.9018, ..., 0.7324, 0.5863, 0.7040],
...,
[0.6274, 0.5709, 0.5410, ..., 0.9458, 0.9812, 0.9870],
[0.5909, 0.6487, 0.5453, ..., 0.8956, 0.9750, 0.9950],
[0.8053, 0.9780, 0.6577, ..., 0.5421, 0.7570, 0.6300]],
device='cuda:0'))
!ls /home/mlaidev/software/jsr_gdm/pytorch_backend/torch_compile_debug/run_2025_05_26_09_03_06_493183-pid_189635/torchinductor/model__1_inference_1.1fx_graph_readable.py fx_graph_transformed.py ir_pre_fusion.txt
fx_graph_runnable.py ir_post_fusion.txt output_code.py